샌드위치 패널의 설계 최적화

2021/10/09 11:06

항공기에서 토목구조물에 이르는 시스템의 레이아웃 해석을 위해서는 복합재 판재의 최적화가 매우 중요합니다. 오늘날의 설계 최적화 번거로움은 샌드위치 복합판에 대한 부담 함수의 최소화입니다. 이것은 최소한의 무게를 주기 위해 샌드위치 층의 두께를 최적화하는 설계 최적화 문제입니다. 현대인에게 특히 흥미로운 것은 설계 변수로 인해 외부 레이어와 코어의 두께가 고려되는 복합 샌드위치 플레이트의 레이아웃 최적화 작업입니다.

Sandwich Panels.jpg

샌드위치 이론 3층 구조의 전형적인 샌드위치 구조 화합물. 외부 레이어는 재료로 만들어집니다 그거 있다 높음 강도 (섬유 강화 라미네이트), 어떤 할 수 있다 전송 축 힘 코어는 폼, 오리나무 등과 같은 경량 재료로 만들어지는 반면 굽힘 모멘트가 있습니다. 샌드위치 코어에 사용되는 재료는 압축에 강하고 전단력을 전달할 수 있어야 합니다. 얇은 커버 시트, 즉 층 1 및 3은 하부 스킨에 대한 두께 h1 및 상부 스킨에 대한 h3을 갖는다. 코어의 두께는 h2입니다(그림 1). 일반적으로 h1은 h3과 같을 필요가 없지만 대칭 샌드위치의 가장 중요한 실제 사례에서는 h1 = h3입니다.

대부분의 샌드위치 구조는 라미네이트 플레이트에 대한 전단 변형 이론을 사용하여 모델링하고 분석할 수 있습니다.

결과 N 및 M에 대해 적분은 시트에 대해서만 수행되고 코어에 대한 가로 전단력에 대해 수행됩니다. 샌드위치에 대한 구성 방정식은 하이퍼매트릭스 형식으로 작성됩니다. 여기서 N, M, V 는 수직항력의 벡터이고,

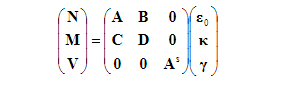
굽힘 모멘트와 횡방향 전단력, γκε,0은 각각 중간 평면 변형률, 곡률 및 횡방향 전단 변형률의 벡터입니다. 강성 계수 ^{는 다음과 같이 계산됩니다. E is}_j 코어의 가로 전단 계수입니다.

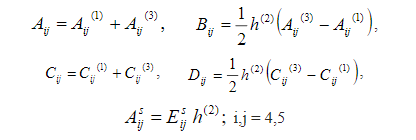
대부분의 샌드위치 구조는를 사용하여 모델링 및 분석전단 변형 이론라미네이트판[1-3]. ||결과N그리고중통합은 시트에 대해서만 수행됩니다.그것은가로 전단 포스 위 코어 코어. 구성 방정식s 용 a 샌드위치 는 작성 에 하이퍼매트릭스 형태씨케이이자형A000D씨0BA안에중N에스0대부분의 샌드위치 구조는를 사용하여 모델링 및 분석전단 변형 이론라미네이트판[1-3]. ||결과N그리고중통합은 시트에 대해서만 수행됩니다.그것은가로 전단 포스 위 코어 코어. 구성 방정식s 용 a 샌드위치 는 작성 에 하이퍼매트릭스 형태씨케이이자형A000D씨0BA안에중N에스0대부분의 샌드위치 구조는를 사용하여 모델링 및 분석전단 변형 이론라미네이트판[1-3]. ||결과N그리고중통합은 시트에 대해서만 수행됩니다.그것은가로 전단 포스 위 코어 코어. 구성 방정식s 용 a 샌드위치 는 작성 에 하이퍼매트릭스 형태씨케이이자형A000D씨0BA안에중N에스0Most sandwich structures can be를 사용하여 모델링 및 분석전단 변형 이론라미네이트판[1-3]. ||결과N그리고중통합은 시트에 대해서만 수행됩니다.그것은가로 전단 포스 위 코어 코어. 구성 방정식s 용 a 샌드위치 는 작성 에 하이퍼매트릭스 형태씨케이이자형A000D씨0BA안에중N에스0